Le plan est muni d'un repère orthonormé.

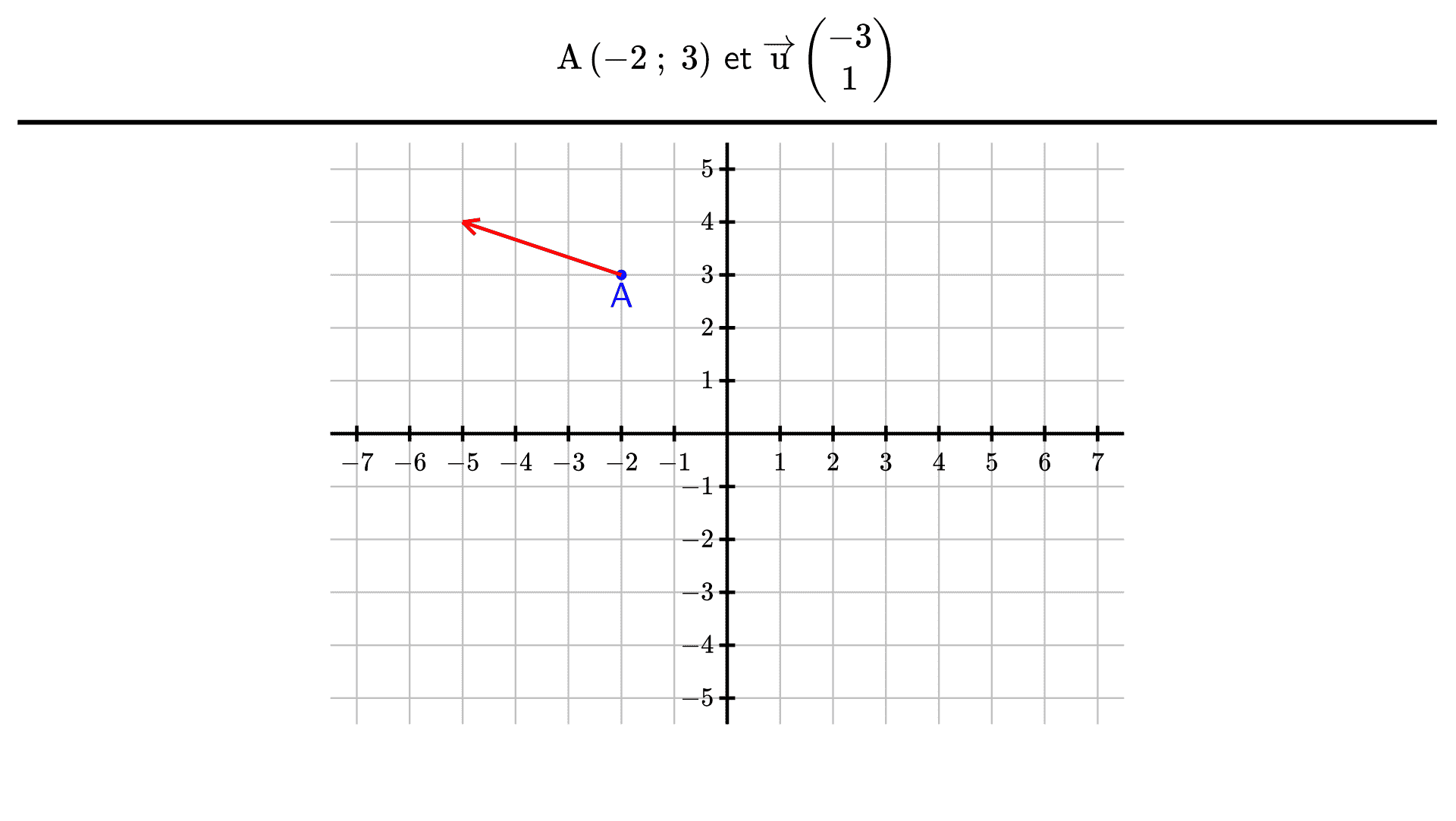
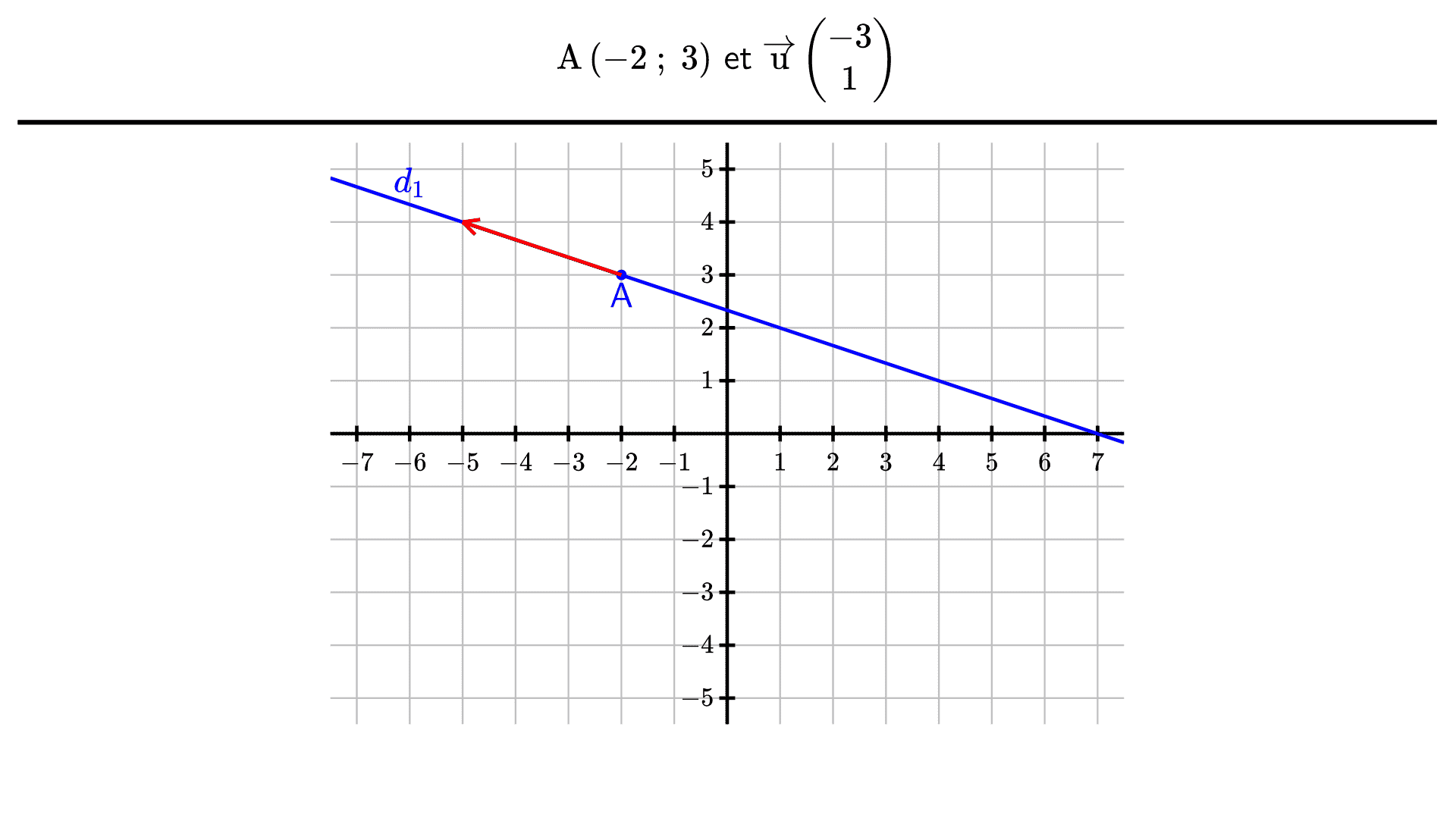
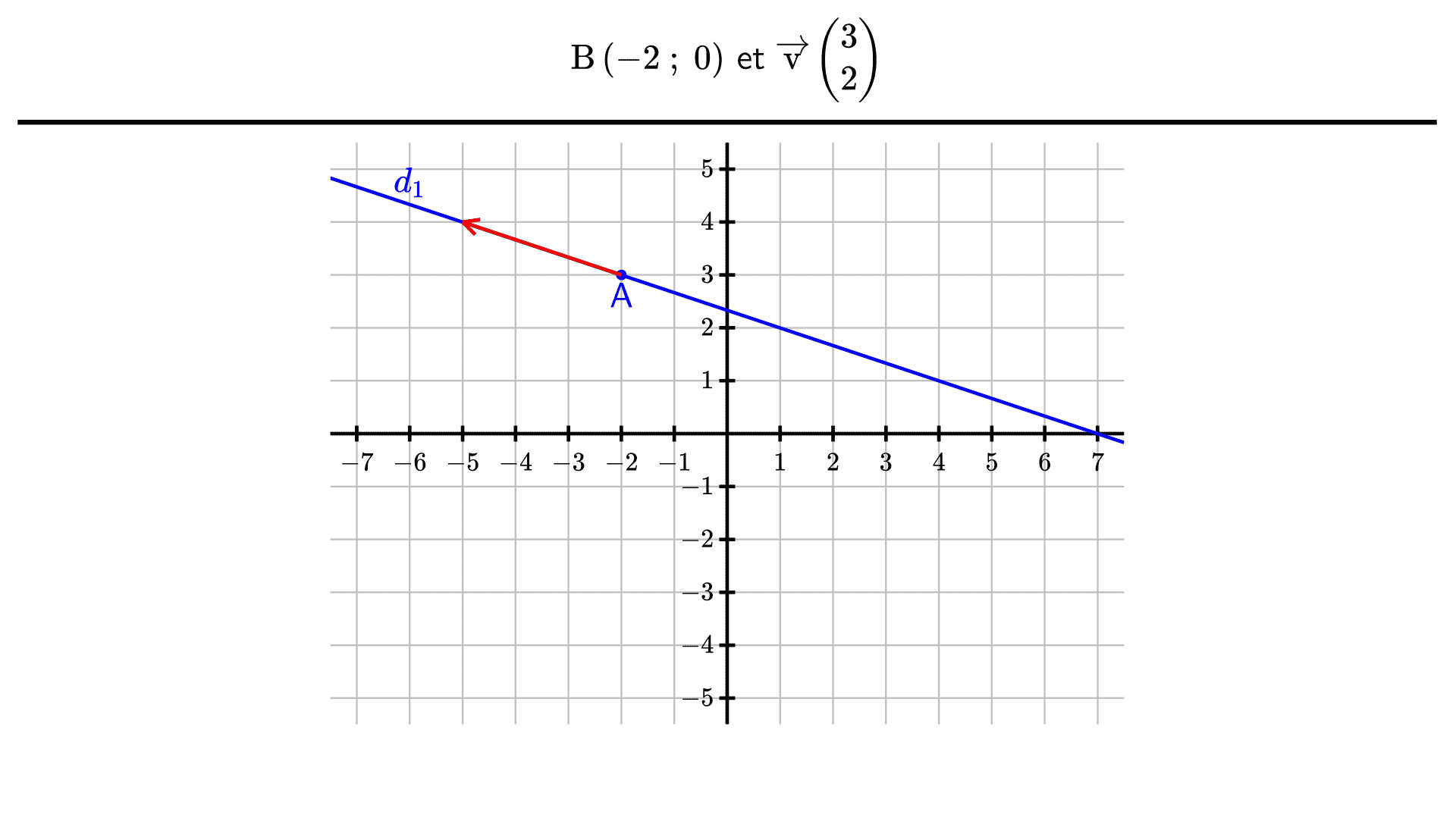
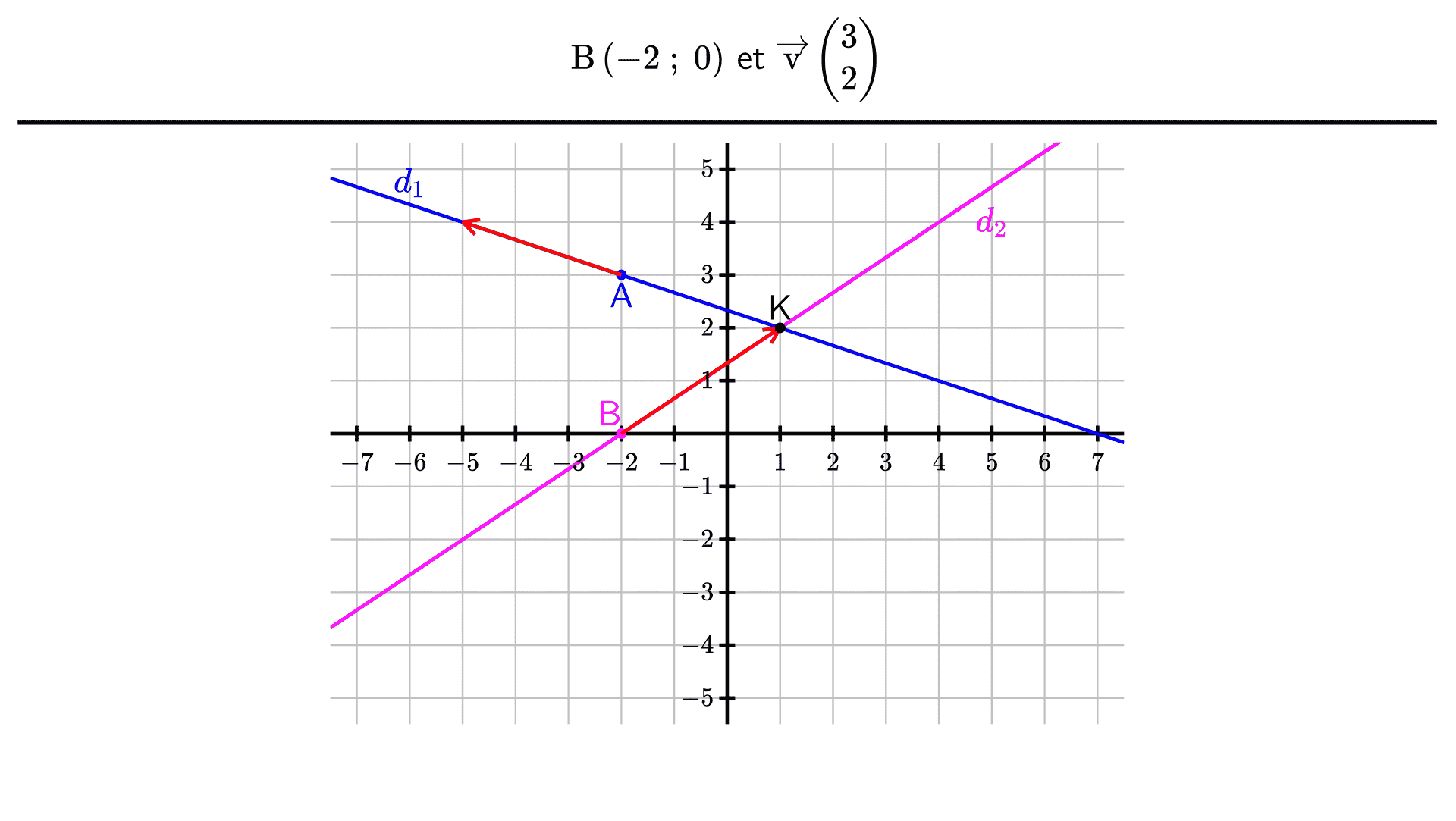
1. Représenter la droite $(d_1)$ qui passe par le point $\mathrm{A}\left(-2 ; 3\right)$ et dont un vecteur directeur est le vecteur $\overrightarrow{\mathrm{u}}\begin{pmatrix}-3\\1\end{pmatrix}$.

2. Déterminer les coordonnées d'un point et d'un vecteur directeur de la droite $(d_2)$ dont voici une équation cartésienne :

   $2x-3y+4=0$

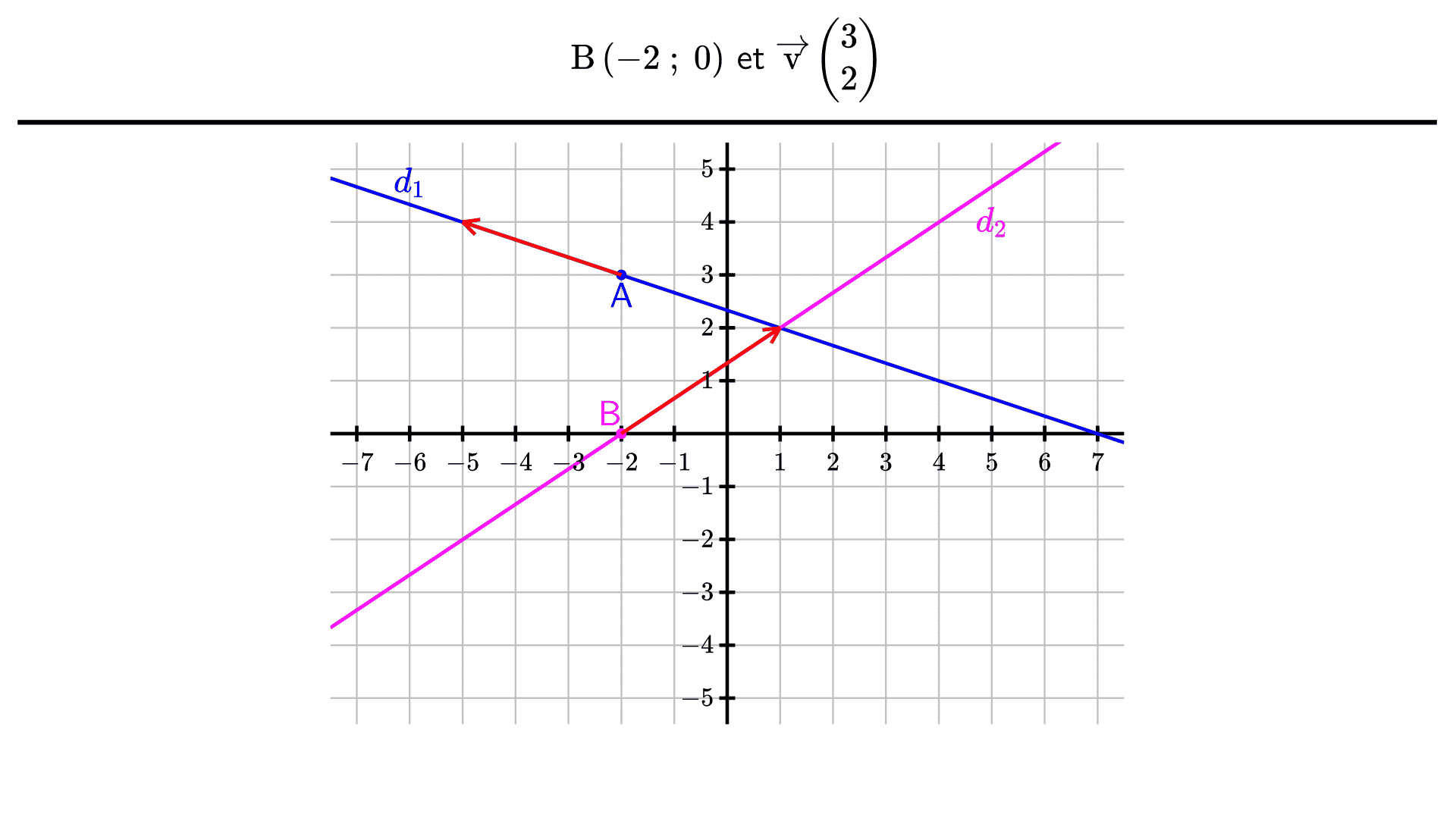
3. Tracer la droite $(d_2)$ sur le même graphique que la droite $(d_1)$.

4. En observant le graphique, conjecturer les coordonnées du point d’intersection des droites $(d_1)$ et $(d_2)$, puis vérifier la conjecture par le calcul.